En el Sistema Solar o en sus sistemas de satélites hay muchas resonancias y cuasi-resonancias. En los sistema de planetas extrasolares, aún hay más. A fecha 25 de noviembre de 2019 había en el catálogo exoplanet del Observatorio de París, 4.133 exoplanetas con 3.073 sistemas planetarios de los que 672 son múltiples. Esto significa que hay 1.732 exoplanetas formando parte de sistemas múltiples. De los 993 pares de exoplanetas que pertenecen al mismo sistema, hay 669 pares resonantes o cuasi-resonantes. Es decir el 67,4% de los pares.
Dos planetas resonantes p/q tienen por la tercera ley de Kepler, una razón de distancias
Si un sistema exoplanetario múltiple tiene todos sus pares de planetas resonantes y da la casualidad de que todas las resonancias son iguales entonces las distancias están en progresión geométrica y el sistema cumple escrupulosamente la ley de Titius-Bode. El problema es que hay 32,6% de pares no resonantes ni cuasi-resonantes. También, que un sistema puede tener todos sus pares resonantes con distintas resonancias, y entonces el mayor o menor error depende fundamentalmente de la disparidad de las resonancias en el sistema y también de su orden. En mucho menos importancia el error depende de que la inmensa mayoría de las veces las resonancias no son exactas. Aunque en general no se cumple la ley de T-B, hay muchos sistemas Kepler resonantes y compactos que la cumplen con errores pequeños.
Si un sistema exoplanetario múltiple tiene todos sus pares de planetas resonantes y da la casualidad de que todas las resonancias son iguales entonces las distancias están en progresión geométrica y el sistema cumple escrupulosamente la ley de Titius-Bode. El problema es que hay 32,6% de pares no resonantes ni cuasi-resonantes. También, que un sistema puede tener todos sus pares resonantes con distintas resonancias, y entonces el mayor o menor error depende fundamentalmente de la disparidad de las resonancias en el sistema y también de su orden. En mucho menos importancia el error depende de que la inmensa mayoría de las veces las resonancias no son exactas. Aunque en general no se cumple la ley de T-B, hay muchos sistemas Kepler resonantes y compactos que la cumplen con errores pequeños.
Pero aquí no vamos a ver la resonancia entre dos planetas, sino entre tres. Ninguna terna de planetas en el Sistema Solar presenta este tipo de resonancia estabilizadora. Sólo tres de los satélites galileanos de Júpiter, los regulares más internos de Urano (Miranda, Ariel y Umbriel) y tres de los satélites de Plutón cumplen la resonancia Laplace.
Se dice que tres planetas de periodos T₁, T₂, T₃ están en resonancia Laplace p:q si cumplen:
donde n son los movimientos medios y p y q números naturales muy sencillos. A diferencia de la resonancia de los movimientos medios, no es preciso que p sea mayor que q. Recordemos que si entre el segundo y el primero hay la misma resonancia p:q de los movimientos medios, que entre el tercero y segundo, entonces también la resonancia Laplace es p:q. Recordemos que hay un ángulo F de libración, que cumplen los longitudes medias de los planetas:
Hay resonancia Laplace p:q entre los planetas P₁, P₂, P₃ si cada p conjunciones de los planetas P₁ y P₂, hay q conjunciones de los planetas P₂ y P₃ y p+q conjunciones de los planetas P₁ y P₃.
Mientras se ha visto la ineficacia de la ley T-B para encontrar probables candidatos a exoplanetas, la resonancia de Laplace ha demostrado su eficiencia intuyendo la existencia de Trappist-1 h y luego la de Kepler-80 g. Posteriormente se encontraron experimentalmente. Esperemos que dicha eficiencia continúe para K2-138.
Se dice que tres planetas de periodos T₁, T₂, T₃ están en resonancia Laplace p:q si cumplen:
F=q𝜆₁-(p+q)𝜆₂+p𝜆₃=A
donde A es 𝜋 o 0, pero si hay varias cadenas Laplace en el mismo sistema veremos que A adquiere otros valores.Hay resonancia Laplace p:q entre los planetas P₁, P₂, P₃ si cada p conjunciones de los planetas P₁ y P₂, hay q conjunciones de los planetas P₂ y P₃ y p+q conjunciones de los planetas P₁ y P₃.
Mientras se ha visto la ineficacia de la ley T-B para encontrar probables candidatos a exoplanetas, la resonancia de Laplace ha demostrado su eficiencia intuyendo la existencia de Trappist-1 h y luego la de Kepler-80 g. Posteriormente se encontraron experimentalmente. Esperemos que dicha eficiencia continúe para K2-138.
1) El sistema Gliese-876
Gliese 876 o GJ 876 es una estrella enana roja de masa 0,334 la masa de nuestro Sol y radio 0,36. Posee cuatro planetas, de los que ignorando al más interior GJ 876 d, los otros tres se hallan en una resonancia Laplace similar a la de los satélites de Júpiter. (Batygin et al. 2015). No obstante la principal diferencia es que los tres planetas Laplace tienen inclinaciones distintas. Gliese 876 b de casi el doble de masa de Júpiter forma un ángulo de 36º con Gliese 876 c y 24,5º con GJ 876 e. Es pues un sistema planetario en tres dimensiones. Es raro para una enana roja tener dos planetas tipo júpiter.
Tabla 1 Los cuatro planetas del sistema Gliese 876. El valor (*) es el periodo sinódico de GJ 876 c y GJ 876 e
Con un error de 0,3 días el periodo para que se repitan las conjunciones de GJ 876 c, b, e es de 119,6 días. Cada 2 conjunciones de GJ 876 c, b hay una conjunción GJ 876 b, e y 3 de GJ 876 c, e.
Así que es una resonancia Laplace 2:1 con resonancias del movimiento medio 1:2:4. El valor de los movimientos medios difiere de 0, sólo -0,0132º/día.
n₁-3n₂+2n₃=0
Y el ángulo F de libración, puede formularse como:
F=𝜆₁-3𝜆₂+2𝜆₃=0=A
con una amplitud A que varia 40º±15°.
2) Kepler-80
Con una estrella con una masa un 70% mayor que el Sol, el sistema Kepler-80 tiene 6 planetas. El último Kepler-80 g descubierto en 2017.
Tabla 2 Los datos del sistema Kepler-80
Cuando en Julio de 2016 Mariah G. MacDonald et. al. publica su trabajo A dynamical analysis of the Kepler-80 system of five transiting planets encuentra dos resonancias Laplace: una formada por Kepler-80 d, e, b y la otra por Kepler-80 e, b, c. El planeta más interno Kepler-80 f se encuentra dinámicamente desacoplado del resto de planetas con resonancias de los movimientos medios iguales o muy parecidas.
Super-periodo
En el trabajo de M.G. MacDonald se dice: La fuerza y el carácter de las variaciones de tiempo de tránsito (TTV) se pueden usar para determinar las masas y las propiedades orbitales, principalmente de los planetas perturbadores. El superperiodo mide la diferencia de la resonancia de primer orden j+1:j entre los planetas correlativos, donde j es un número entero.
donde P y P '> P son los períodos orbitales de los dos planetas (Agol et al. 2005; Lithwick et al. 2012). El super-periodo es el tiempo en que las TTV empiezan a repetirse.
En el caso de Kepler-80, el superperíodo para cada uno de los tres pares vecinos de los cuatro planetas exteriores es de ~191 días. Los cuatro planetas exteriores de Kepler-80 muestran TTVs estadísticamente significativos con un carácter similar a muchos otros sistemas Kepler TTV: sinusoides anti-correlacionados con un "superperíodo" igual al tiempo que tarda la conjunción de dos planetas correlativos (si los planetas no tuvieran masa). Es decir, el tiempo que tardan dos planetas adyacentes en el sistema Kepler-80, en tener tránsito simultáneamente El hecho de que varios pares compartan el mismo superperíodo es una característica especial del sistema Kepler-80, equivalente a la configuración de resonancia múltiple de tres cuerpos de Laplace.
Las observaciones de Kepler abarcan múltiples superperíodos de conjunción de 191 días, pero no cubren un ciclo completo de libración por resonancia de tres cuerpos.
La primera cadena
Tabla 3 El (*) se refiere al periodo sinódico Kepler-80 d, b
Hay un múltiplo de los periodos sinódicos 27,1 d con un error de 0,1 d .Ocurren 3 conjunciones de Kepler-80 d, e por cada 2 conjunciones Kepler-80 e, b y 5 conjunciones Kepler-80 d, b. La resonancia Laplace es 3:2 .Por tanto el ángulo de libración cumple:
Tabla 4 El (*) se refiere al periodo sinódico Kepler-80 e, c
Hay un múltiplo de los periodos sinódicos 27,1 d con un error de 0,08 d .Ocurren 2 conjunciones de Kepler-80 e, b por cada conjunción Kepler-80 b, c y 3 conjunciones Kepler-80 e, c. La resonancia Laplace es 2:1. Por tanto el ángulo de libración cumple:
Como el periodo para las dos cadenas es el mismo 27,1 días podemos afirmar que:
Ocurren 3 conjunciones de Kepler-80 d, e por cada 2 conjunciones Kepler-80 e, b, 5 conjunciones Kepler-80 d, b, 1 conjunción Kepler-80 b, c y 3 conjunciones Kepler-80 e, c.
Cuando en Julio de 2016 Mariah G. MacDonald et. al. publica su trabajo A dynamical analysis of the Kepler-80 system of five transiting planets encuentra dos resonancias Laplace: una formada por Kepler-80 d, e, b y la otra por Kepler-80 e, b, c. El planeta más interno Kepler-80 f se encuentra dinámicamente desacoplado del resto de planetas con resonancias de los movimientos medios iguales o muy parecidas.
Super-periodo
En el trabajo de M.G. MacDonald se dice: La fuerza y el carácter de las variaciones de tiempo de tránsito (TTV) se pueden usar para determinar las masas y las propiedades orbitales, principalmente de los planetas perturbadores. El superperiodo mide la diferencia de la resonancia de primer orden j+1:j entre los planetas correlativos, donde j es un número entero.
donde P y P '> P son los períodos orbitales de los dos planetas (Agol et al. 2005; Lithwick et al. 2012). El super-periodo es el tiempo en que las TTV empiezan a repetirse.
En el caso de Kepler-80, el superperíodo para cada uno de los tres pares vecinos de los cuatro planetas exteriores es de ~191 días. Los cuatro planetas exteriores de Kepler-80 muestran TTVs estadísticamente significativos con un carácter similar a muchos otros sistemas Kepler TTV: sinusoides anti-correlacionados con un "superperíodo" igual al tiempo que tarda la conjunción de dos planetas correlativos (si los planetas no tuvieran masa). Es decir, el tiempo que tardan dos planetas adyacentes en el sistema Kepler-80, en tener tránsito simultáneamente El hecho de que varios pares compartan el mismo superperíodo es una característica especial del sistema Kepler-80, equivalente a la configuración de resonancia múltiple de tres cuerpos de Laplace.
Las observaciones de Kepler abarcan múltiples superperíodos de conjunción de 191 días, pero no cubren un ciclo completo de libración por resonancia de tres cuerpos.
La primera cadena
Hay un múltiplo de los periodos sinódicos 27,1 d con un error de 0,1 d .Ocurren 3 conjunciones de Kepler-80 d, e por cada 2 conjunciones Kepler-80 e, b y 5 conjunciones Kepler-80 d, b. La resonancia Laplace es 3:2 .Por tanto el ángulo de libración cumple:
Φ1 ≡ 2λd−5λe+ 3λb (p = 3, q = 2)
La segunda cadena
Hay un múltiplo de los periodos sinódicos 27,1 d con un error de 0,08 d .Ocurren 2 conjunciones de Kepler-80 e, b por cada conjunción Kepler-80 b, c y 3 conjunciones Kepler-80 e, c. La resonancia Laplace es 2:1. Por tanto el ángulo de libración cumple:
Como el periodo para las dos cadenas es el mismo 27,1 días podemos afirmar que:
Φ2 ≡ λe −3λb +2λc (p = 2, q = 1)
Ocurren 3 conjunciones de Kepler-80 d, e por cada 2 conjunciones Kepler-80 e, b, 5 conjunciones Kepler-80 d, b, 1 conjunción Kepler-80 b, c y 3 conjunciones Kepler-80 e, c.
Encontramos que las cuatro posibles configuraciones de resonancia de tres cuerpos de Kepler-80 son liberadoras con amplitudes de solo unos pocos grados (ver Figura 5), lo que muestra claramente que el sistema es profundo en resonancias de tres cuerpos.
Debido a la naturaleza entrelazada de las resonancias, hay muchas proporciones de tres cuerpos que varían lentamente en este sistema. Sin embargo, la resonancia 1: –2: 1 entre d, e y c y la resonancia 1: –6: 5 entre d, c y b son comparativamente fuertes (ver Figura 5 y discusión a continuación). Muchas combinaciones lineales de estos ángulos de resonancia también son liberadoras, lo cual es fácil de mostrar matemáticamente y lo hemos confirmado mediante inspección. Los argumentos de Quillen y French (2014) sugieren que todo esto puede contribuir a la evolución dinámica y la estabilidad del sistema.
Las fases de los planetas son tales que nunca hay una conjunción triple o cuádruple con tres planetas alineados, lo que probablemente sea un mecanismo de protección resonante que ayuda a garantizar la estabilidad a largo plazo. Hay un momento en que d y b están alineados y e está alineado, lo que tiene similitud con la configuración de los satélites galileanos y se repite con un período de 191 días. Otra configuración interesante ocurre cuando los dos planetas externos (b / c) tienen una conjunción: en este momento, los dos planetas internos (d / e) están anti-alineados y las líneas de conjunción b / c y d / e están a casi 90 grados de unos y otros.
Tenga en cuenta que los cuatro ángulos de resonancia identificados en el párrafo anterior y que se muestran en la Figura 5 no liberan alrededor de 0 o 180 grados como se esperaba teóricamente para resonancias aisladas de tres cuerpos; sin embargo, la libración alrededor de un centro diferente es común en sistemas de varios planetas. Se ve, por ejemplo, en Kepler-223 Mills et al.) y es causado por un par del otro planeta no resonante que desplaza el centro de resonancia.
Las pequeñas amplitudes de libración de las resonancias de tres cuerpos de Kepler-80 imponen fuertes restricciones sobre la formación y la historia dinámica pasada de este sistema.
En Identifying exoplanets with deep learning: a five planet resonant chain around Kepler-80 and an eighth planet around Kepler-90 de Christopher J. Shallue et. al.dicen que la resonancia Laplace para ayudar a encontrar al planeta Kepler-80 g
Recientemente, se uso el superperiodo por Luger et al. (2017) para predecir y recuperar el período orbital del planeta TRAPPIST-1 h utilizando datos de la misión K2. Siguiendo a Luger et al. (2017), calculamos los períodos orbitales de los supuestos planetas externos adicionales en el sistema Kepler-80 bajo el supuesto de que ocurrieron en una resonancia de tres cuerpos con Kepler-80 b y c. La ecuación de la resonancia Laplace tras introducir los valores de p y q entre 1 y 3 (inclusive), permite identificar posibles períodos orbitales de 14.64671, 11.54078, 10.77887, 31.72031, 12.41860 y 20.04003 días. Efectivamente con T₁=7,05 d y T₂=9,52 días resulta
Tabla 5 Distintos periodos de Kepler-80 g atendiendo a las diferentes resonancias Laplace.
Para p = q = 1, el período pronosticado por la relación de Laplace está dentro de los 100 segundos del período orbital medido (14,64558 ± 0,00012 días) del planeta recién descubierto - acuerdo dentro de una parte en 10.000. Kepler-80 g orbita justo fuera de una relación de período 3: 2 con el planeta de 9,52 días, y estos dos planetas tienen un súper período de 192 días, que coinciden con los súper períodos de otros pares de planetas en el sistema. Kepler-80 g, por lo tanto, casi con toda seguridad es parte de la cadena de resonancias de tres cuerpos alrededor de Kepler-80, lo que eleva el número total de planetas en la cadena a 5 y el número total de planetas en el sistema a seis. El hecho de que podamos predecir con tanta precisión el período orbital de Kepler-80 g a través de argumentos de resonancia es una fuerte confirmación independiente de que la señal es causada por un exoplaneta, y una validación de nuestros métodos de extremo a extremo.
Kepler-80 g garantiza un mayor estudio por varias razones. Primero, aunque el período orbital que encontramos hace que sea extremadamente probable que este planeta recién descubierto sea el eslabón externo en una cadena de resonancias de tres cuerpos, el sistema requiere un análisis dinámico adicional para confirmar la resonancia estado. Aunque su baja relación señal / ruido lo dificultará, podría valer la pena buscar las variaciones de tiempo de tránsito de Kepler-80 g, tal vez midiendo el tiempo de muchos tránsitos promediados juntos (por ejemplo, Mills et al.2016). Finalmente, será importante evaluar el impacto de un nuevo planeta en la cadena resonante en las mediciones de masa Kepler-80 TTV realizadas por MacDonald et al. (2016) En principio, si parte de la señal de TTV medida en el Kepler-80 c de 9.52 días fue causada por Kepler-80 g, eso afectaría la masa medida de Kepler-80 b, y así sucesivamente.
La tercera cadena
Φ3 ≡ λb −2λc + λg (p = 1, q = 1)
3) Kepler-223
Poco se conoce de la estrella Kepler-223. Su radio con mucha incertidumbre es 1,02 y su masa deducida de la tercera ley de Kepler es 0,946 la solar, así que debe ser una estrella similar al Sol de metalicidad -0,211. A su alrededor giran cuatro planetas descubiertos por tránsito en 2014 por el telescopio espacial Kepler. Sólo se conoce el radio que oscila entre 1,69 y 2,97 veces el radio de la Tierra por lo que se trata de neptunos y neptunos ligeros es decir planetas gaseosos quizá hinchados por orbitar cerca de su estrella ya que sus períodos van de sólo 7 a 19 días.
Los cuatro planetas de Kepler-223 están en resonancia orbital es decir sus periodos orbitales guardan una relación numérica sencilla. Podemos decir que los cuatro planetas están en una resonancia conjunta 1,4/3, 2,8/3 o quitando denominadores 3:4:6:8.
A mi modesto entender estos planetas del sistema Kepler-223 se parecen más a los satélites galileanos. Para ver la similitud expresaremos las distancias del planeta a su estrella en radios de la estrella. La constante de Kepler se expresará en la unidad especial días²/ radios estrella³ .
Tabla 7 Características de los planetas de Kepler-223.
Lo que puede extrañar más es que en estas unidades la constante de Kepler valga aproximadamente lo mismo en los dos. Si expresamos las masas en veces la masa del Sol, el periodo en años y la distancia en U.A. la constante vale 1 para los planetas del Sistema Solar y 1/M para los extrasolares. Pero si el tiempo lo expresamos en la misma unidad y la distancia en radios de la estrella la constante depende de R³/M donde R es el radio de la estrella en radios solares y M la masa. Así la constante depende de la densidad de la estrella. Como las densidades de la estrella y del planeta Júpiter son muy parecidas se produce esta igualdad.
En un trabajo titulado A Resonant Chain of Four Transiting, Sub-Neptune Planets Sean M. Mills et. al. hablan de la resonancia Laplace de este primer sistema resonante con cuatro planetas. De la medición de los tiempos TTV causados por la masa de los otros tres y de la medición de dichas masas.
Podemos distinguir dos cadenas resonantes Laplace.
1ª cadena
Tabla 8 El (*) se refiere al periodo sinódico Kepler-223 b, d
Hay un múltiplo del periodo sinódico de 29,5 días con un error de 0,03 días. Por cada conjunción de Kepler-223 b, c hay una conjunción de Kepler-223 c, d y 2 conjunciones de Kepler-223 b, d. La resonancia Laplace es 1:1 pero el comportamiento de la cadena resonante puede caracterizarse por sus ángulos de Laplace que parecen asignarle una resonancia Laplace –1:-1:
Φ1 ≡ −λb + 2λc − λd
2ª cadena 
Tabla 9 El (*) se refiere al periodo sinódico Kepler-223 c, e
Hay un múltiplo del periodo sinódico de 59,0 días con un error de 0,03 días. Por cada 2 conjunciones de Kepler-223 c, d hay una conjunción de Kepler-223 d, e y 3 conjunciones de Kepler-223 c, e. La resonancia Laplace es 2:1 y el comportamiento de la cadena resonante
Φ2 ≡ λc − 3λd + 2λe así lo confirma.
Para todo el sistema de cuatro planetas, ( b, c, d, e) Φ3 ≡ 2Φ2 −3Φ1 = 3λb −4λc −3λd + 4λe.
Para todo el sistema de cuatro planetas, ( b, c, d, e) Φ3 ≡ 2Φ2 −3Φ1 = 3λb −4λc −3λd + 4λe.
Si asumimos órbitas casi circulares, los cuatro años de TTV en los datos han registrado ambos ángulos realizando casi una oscilación completa; Φ1 libra entre aproximadamente 173º y 190º y Φ2 libra entre aproximadamente 47º y 75º.
Esto garantiza que dos planetas tengan un acercamiento cercano cuando los otros planetas están muy lejos, lo que reduce las interacciones caóticas.
4) Trappist-1
En el trabajo de Rodrigo Luger et. al. publicado con el título A seven-planets resonant chain in Trappist-1 dice: Llevamos a cabo tres búsquedas de tránsito separadas en la curva de luz de cadencia larga, con el objetivo de buscar el período de TRAPPIST-1h, que solo se había observado que transita una vez, así como para encontrar planetas adicionales en el sistema. Un análisis dinámico realizado por nuestro equipo antes del de publicar los datos de K2 sugirieron ciertos valores del período de TRAPPIST-1h basados en la presencia de resonancias Laplace entre tres de los planetas.
Entre los seis planetas interiores en TRAPPIST-1, hay cuatro conjuntos adyacentes de tres planetas que satisfacen esta relación para 1 ≤ q ≤ 2 y 1 ≤ p ≤ 3 (Tabla 1). En el trabajo original de Rodrigo Luger los papeles de p y q están cambiados. Aquí usaremos la notación de este trabajo. En la tabla al ser captura de pantalla no los hemos podido modificar.
Hay sistemas compactos, resonantes y con varias cadenas Lagrange en que es el superperiodo es un elemento clave para determinar las VTT y permitir hallar las masas mediante el método del tránsito.
Veamos las cadenas Lagrange es este sistema. No encontraremos otro con 5 cadenas Lagrange.
En efecto 1ª cadena
Tabla 10 Las 5 cadenas Lagrange del sistema planetario Trappist-1.
Esta sugirió que el período del planeta TRAPPIST-1h también puede satisfacer una resonancia de tres cuerpos con TRAPPIST-1 f y g. Los seis períodos potenciales de TRAPPIST-1h que satisfacen las relaciones de tres cuerpos.
Con 1 ≤ p, q ≤ 3 son 18,766 d (p = q = 1), 14,899 d (p =2, q = 1), 39,026 d (p = 1, q = 2), 15,998 d (p = 3, q = 2), 13,941 d (p = 3, q = 1) y 25,345 d (p = 2, q =3). Examinamos ~1000 horas de datos en tierra tomadas antes del conjunto de datos Spitzer2 y encontraron una falta de evidencia.
Tabla 11 Con T1=9,20669 (TRAPPIST-1 f ) y T2=12,35294 (TRAPPIST-1 g) tenemos según p y q los periodos T₃ de TRAPPIST-1 h. Se comparan con los valores del trabajo. El valor real del periodo de Trappist-1 h es 18,77 días que corresponde a la resonancia Laplace 1:1.
Los tránsitos adicionales en los tiempos esperados para todos estos períodos, salvo 18,766 d. El periodo de 18,766 d corresponde a tiempos de tránsito anteriores en ventanas que se perdieron en el terreno anterior campañas basadas; por lo tanto, este fue el único período que no se pudo descartar. Además, como esto el valor es consistente con el período estimado de 20 + 15 d basado en la duración del tránsito de Spitzer.
Teníamos razones para creer que era el período correcto para TRAPPIST-1h. Para probar esta hipótesis, en nuestra primera búsqueda de tránsito simplemente doblamos la curva de luz de cadencia larga en los cuatro tiempos de tránsito esperados dado este período y el tiempo de tránsito único de Spitzer, encontrando evidencia de un planeta en tránsito en ese período. El seguimiento con datos de cadencia corta sin tendencia confirma la forma de tránsito de cada uno de los cuatro eventos y una profundidad consistente con la de TRAPPIST-1h (ver Métodos).
5) HD 158259
Es un sistema de 4 planetas y un quinto, el más exterior, candidato que orbita un estrella un 8% más masiva que el Sol. Se ha descubierto en 2019 por VR así que las masas son las mínimas.
Tabla 12 El sistema HD 158259. El planeta HD 158259 f es un candidato.
En 2019 Hara N. et. al. publicaron el artículo
titulado The SOPHIE search for northern
extrasolar planets. XVII. A compact planetary system in anear 3:2 mean motion resonance chain en él dicen:
En segundo lugar, HD 158259 c se encuentra entre los dos MMR
3: 2, con los planetas b y d.
Si bien los planetas en el sistema HD 158259 están claramente
fuera de los 3: 2 MMR, aún podrían bloquearse en resonancias de tres planetas, resonancias
Laplace. En efecto
1ª
cadena
Tabla 13 El (*) se refiere al periodo sinódico HD 158259 b, d
Hay un múltiplo del periodo sinódico de 30,2 días
con un error de 0,12 días. Por cada 3 conjunciones de HD 158259 b, c hay dos conjunciones de HD 158259 c, d y 5
conjunciones de HD 158259 b, d.
La resonancia Laplace es 3:2 y el comportamiento de la cadena resonante
Φ123
= 2λ1 −5λ2 +3λ3 ≈ π,
Tabla 14 El (*) se refiere al periodo sinódico HD 158259 c, e
Hay un múltiplo del periodo sinódico de 45,9 días
con un error de 1,95 días. Por cada 3 conjunciones de HD 158259 c, d hay dos conjunciones de HD 158259 d, e y 5
conjunciones de HD 158259 c, e.
La resonancia Laplace es 3:2 y el comportamiento de la cadena resonante
Φ234 = 2λ2−5λ3
+3λ4 ≈ π,
donde λi es la longitud media del planeta i,
ambos deberían librar alrededor de π. Además, si estos ángulos se libran, sus
derivados deberían promediar a cero durante el período de libración (por
ejemplo, Mills et al.2016) donde Pi es el período orbital del planeta i.
Observamos las distribuciones de F123 F234,
así como sus derivados en las partes posteriores del MCMC y concluimos que el
sistema tampoco está bloqueado en estas resonancias de Laplace.Sin embargo, las relaciones de período tan
cercanas a 3: 2 no pueden explicarse por pura aleatoriedad. Por lo tanto, es
probable que durante la migración de los planetas en el disco protoplanetario,
se encerraron en una cadena de 8: 12: 18: 27 (con cada par consecutivo de
planeta encerrado en 3: 2 MMR). La desviación observada actualmente de la
conmensurabilidad exacta podría explicarse por la disipación de las mareas, ya
que ya se propuso para sistemas Kepler similares (por ejemplo, Delisle y Laskar)
El planeta candidato HD 158259 f o bien no existe
o no tiene ese periodo o no forma una resonancia Laplace con HD 158259 d, e.
6)
K2-138
En enero de 2018 se publicó The K2-138 System: A Near-Resonant Chain Of Five Sub-Neptune Planets Discovered By Citizen Scientists de Jessie L.
Christiansen et. al. (enlace ) en él los autores hablan de un sistema totalmente resonante con una cadena
ininterrumpida de resonancias cercanas a 3:2. El planeta K2-138 g no figura en este
trabajo. Fue descubierto ese mismo año y rompe esta cadena.
Jessie
L. Christiansen también habla de tres cadenas Laplace de los cinco planetas
entonces conocidos: K2-138 b, c, d K2-138 c, d, e y
K2-138 d, e, f.
En
efecto, 1ª cadena Laplace
Tabla 16 Las tres cadenas Laplace del sistema K2-138
Especulación:
¿Podría haber un planeta entre K2-138 f y g que hiciese el
sistema totalmente resonante? La contestación es que hay varias soluciones 3:2
y 9:4, 2:1 y 5:3 o su simétrica o incluso con dos planetas 3:2, 3:2 y 3:2 que
lo convertiría en un hipotético sistema de 8 planetas con una cadena ininterrumpida de siete resonancias
3:2.
Limitándonos a un sólo hipotético planeta K2-138 h
para seguir la cadena de resonancias Laplace, el periodo de K2-138 h sería:
Tabla 17 Periodo propuesto segun la resonancia Laplace p:q para el hipotético planeta K2-138 h en el supuesto de que K2-138 e, f, h formen una resonancia Laplace.
Pero ninguno de estos periodos para K2-138 h haría
que el sistema K2-138 f ,
h y g fuera resonante Laplace. Podría
haber 4 cadenas Laplace pero nunca 5 con la suposición de un sólo planeta
adicional. El error mínimo en el múltiplo sería de 3,13 días en el caso de una
resonancia Laplace 3:2 en la cadena K2-138 e, f, h y una resonancia Laplace 1:1
la cadena K2-138 f ,
h, g.
Si hubiese dos planetas hipotéticos entre K2-138 f y K2-138 g con resonancia
aproximada 3:2 podríamos exigir que
K2-138 e, f, h1 fuese resonante Laplace 3:2 y entonces el periodo de K2-138 h1
sería Th1=20,0219 días. También
podríamos exigir que K2-138 h1, h2, g fuese resonante Laplace y entonces Th2=29,176 días. Pero entonces, se puede comprobar que, K2-138 f , h1, h2 dista mucho de
la resonancia Laplace. Es decir con dos planetas hipotéticos podemos lograr una cadena de 7 resonancias 3:2
ininterrumpida pero sólo 5 resonancias Laplace 3:2, nunca seis.
7)
Comparación sistemas HD
158259 y K2-138
Encontrar dos sistemas que respecto a la sucesión de
periodos sean similares es muy improbable. No obstante siempre se puede
multiplicar las distancias o periodos por un factor de escala para hacerlos
comparables. Eso no hace falta con HD 158259 y K2-138.
A
finales de 2019 el astrofísico francés Alexandre Santerne anunció mediante un tuit el descubrimiento de un nuevo
exoplaneta, aún no publicado, al que hemos llamado HD 158259 g de periodo 2,18 días
y que mantiene, con el hasta ahora más interior, una razón de periodos 1,5743289
cercano a 3/2. Alexandre Santerrne establece
una comparación entre los sistemas HD 158259 y K2-138
pues ambos son sistemas resonantes 3/2 con dos y tres cadenas de resonancia
Laplace. Si el planeta más interior
tiene un periodo similar (2,18 y 2,35 días respectivamente) ambos sistemas
se pueden comparar. Para ello mantendremos la existencia de los planetas
hipotéticos K2-138
h1 y K2-138 h2 de periodos Th1=20,0219 días y Th2=29,176 días para hacer que K2-138 e, f, h1 y K2-138
h1, h2, g sean cadenas resonante Laplace 3:2.
En cuanto a HD 158259 admitimos la existencia del candidato HD 158259 f y el
descubrimiento de HD 158259
g . Ello permite establecer una comparación entre ambos
sistemas planetarios:
Tabla 18 Comparación de los sistemas HD 158259 y K2-138 asumiendo que HD 158259 g es un exoplaneta descubierto por Tess, que existen K2-138 h1 y h2 con esos periodos para cumplir que forman cadenas Laplace.
Fig 1 Dibujando los logaritmos de los periodos de HD 158259 y K2-138 contra el
número de orden en los supuestos anteriores. Con ellos ambos sistemas forman una cadena ininterrumpida de resonancias de los movimientos medios 3:2 así que cumplen la ley de T-B y son paralelas. Son casi coincidentes porque el periodo del planeta interior es casi coincidente 2,18 frente a 2,35 días.
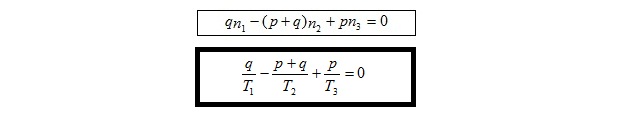
No hay comentarios:
Publicar un comentario